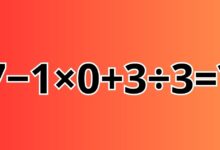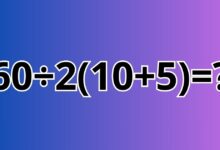Zagadki matematyczne są świetnym sposobem na rozwijanie umiejętności logicznego myślenia i spostrzegawczości. Jednym z takich przykładów jest poniższa łamigłówka, która wymaga znalezienia brakującej liczby w symetrycznym układzie liczb. Przyjrzyjmy się tej zagadce krok po kroku, aby odkryć, jaki wzór kryje się za rozmieszczeniem liczb.
Jaka jest brakująca liczba?
Przedstawiona łamigłówka składa się z kwadratu, w którym umieszczono liczby. W środku znajduje się liczba 8, otoczona przez inne liczby w układzie symetrycznym. Naszym zadaniem jest ustalenie brakującej liczby, oznaczonej znakiem zapytania.
Aby znaleźć brakującą liczbę, musimy dokładnie przeanalizować wzór, jaki tworzą pozostałe liczby. Przyjrzyjmy się sumom liczb na poszczególnych liniach segmentów:
- Górny segment: 9 + 1 + 5 = 15
- Lewy segment: 9 + 4 + 2 = 15
- Prawy segment: 5 + 3 + 7 = 15
- Diagonalny segment (od lewego górnego do prawego dolnego): 9 + 8 + 7 = 24
Widać, że suma liczb w segmentach górnym, lewym i prawym wynosi 15. Aby zachować spójność wzoru, suma liczb w dolnym segmencie również powinna wynosić 15. Dolny segment wygląda następująco: 2 + ? + 7.
Obliczmy brakującą liczbę:
2 + ? + 7 = 15
2 + 7 = 9
15 – 9 = 6
Zatem brakującą liczbą jest 6.
Rozwiązanie tej zagadki wymagało analizy sum liczb w różnych segmentach układu. Kluczowym elementem było zauważenie, że sumy te są równe 15, co pozwoliło nam na obliczenie brakującej liczby. Takie zagadki nie tylko dostarczają satysfakcji z rozwiązania, ale także pomagają w rozwijaniu umiejętności matematycznych i logicznych. Zachęcamy do rozwiązywania kolejnych łamigłówek, które mogą być równie fascynujące i pouczające.