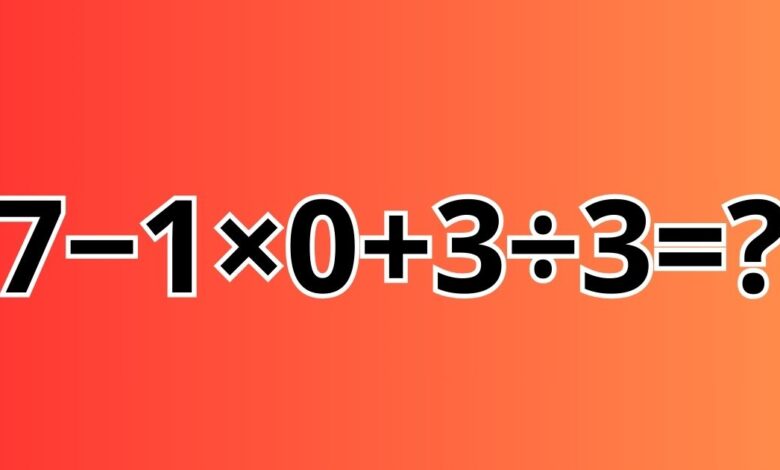
Czy kiedykolwiek zastanawiałeś się, dlaczego proste równania mogą czasem sprawiać tyle trudności? Odpowiedź leży w zasadach pierwszeństwa działań matematycznych, znanych również jako kolejność operacji. Prawidłowe stosowanie tych zasad jest kluczem do rozwiązania naszego równania. Zanim jednak przejdziemy do rozwiązania, przypomnijmy sobie podstawowe reguły kolejności operacji.
Zagadka matematyczna
Matematyka, z jej precyzyjnymi regułami i logicznymi zasadami, bywa czasem źródłem ciekawych zagadek, które potrafią wywołać gorące dyskusje nawet wśród najbardziej doświadczonych matematyków. Jednym z takich problemów jest niewinnie wyglądające równanie:
7−1×0+3÷3=?
Na pierwszy rzut oka, może się wydawać, że odpowiedź jest prosta, ale zaskakująco wielu ludzi popełnia błąd przy próbie jego rozwiązania. Przyjrzyjmy się bliżej tej zagadce i zobaczmy, jak poprawnie ją rozwiązać.
W matematyce obowiązuje ustalona kolejność wykonywania działań, często zapamiętywana przy pomocy akronimu PEMDAS:
- P – Nawiasy (Parentheses)
- E – Potęgowanie (Exponents)
- MD – Mnożenie i Dzielenie (Multiplication and Division) – od lewej do prawej
- AS – Dodawanie i Odejmowanie (Addition and Subtraction) – od lewej do prawej
Przyjrzyjmy się teraz, jak te zasady zastosować do naszego równania.
Rozwiązanie
Nasze równanie to:
7−1×0+3÷3
Zgodnie z zasadami kolejności operacji, najpierw wykonujemy mnożenie i dzielenie, a następnie dodawanie i odejmowanie. Spójrzmy na to krok po kroku:
- Mnożenie: 1×0=0
- Równanie po wykonaniu mnożenia wygląda tak: 7−0+3÷3
- Dzielenie: 3÷3=1
- Równanie po wykonaniu dzielenia: 7−0+1
- Odejmowanie i Dodawanie:
- 7−0=7
- 7+1=8
Ostateczne rozwiązanie równania to:
7−1×0+3÷3=8
Jak widzimy, klucz do rozwiązania tej matematycznej zagadki tkwi w przestrzeganiu zasad kolejności operacji. Bez względu na to, jak prosto wygląda równanie, zawsze warto przypomnieć sobie podstawowe reguły matematyki. W ten sposób unikniemy błędów i szybko znajdziemy poprawne rozwiązanie.