W sieci możemy znaleźć mnóstwo łamigłówek, nad którymi można zastanawiać się godzinami. Niektóre z nich są wyjątkowo trudne i możliwe do rozwiązania tylko przez wyjątkowo spostrzegawcze osoby.
Jeden z testów przykuł naszą uwagę w sposób szczególny. To nie lada wyzwanie, które pozwoli zarówno miło spędzić czas, jak i ćwiczyć swój mózg! Sprawdź, czy potrafisz wskazać właściwe rozwiązanie!
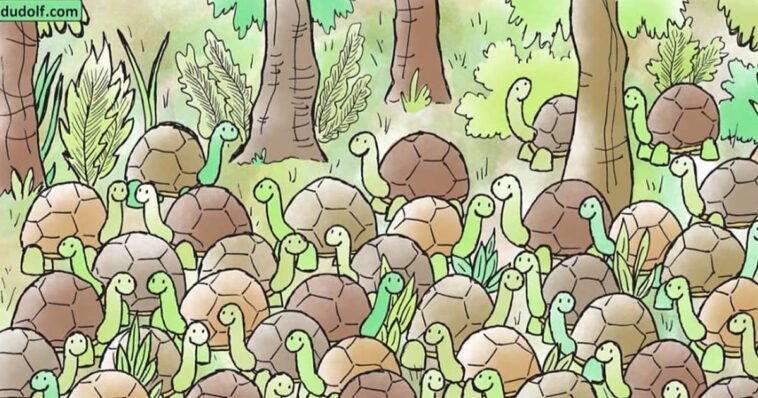
Gdzie jest wąż?
Testy na spostrzegawczość są niezwykle popularne w Internecie. Nic dziwnego – to wspaniała forma rozrywki i dobry sposób na sprawdzenie swoich umiejętności.
Czy potrafisz znaleźć na poniższym obrazku węża? Warto podkreślić, że wyjątkowo dobrze się ukrył! Jego znalezienie nie będzie łatwym zadaniem. Warto podkreślić, że wąż kryje się pośród innych zwierząt. To sprawia, że jego znalezienie staje się jeszcze trudniejsze. Skup się i nie poddawaj zbyt łatwo!
Zagadka została opublikowana i przygotowana przez węgierskiego rysownika Gergely’a Dudasa (Dudolf). Artysta z pewnością nie zdawał sobie sprawy z tego, że jego łamigłówka wywoła takie zamieszanie!
Oto rozwiązanie:
Udało ci się? Pochwal się w komentarzu!
Nie zapomnij podzielić się tą łamigłówką ze swoimi znajomymi!